なんでも数式で解いてみる「ルジャンドル予想」

ルジャンドル予想をご存知でしょうか？

任意の自然数 n について、n² と (n + 1)² の間には
必ず素数が存在する。という予想である。

素数ベースなので素数を準備する
数式は簡単なのですが素数は規則的に取得できないので
素数 99991（9592行）まで計算してみました





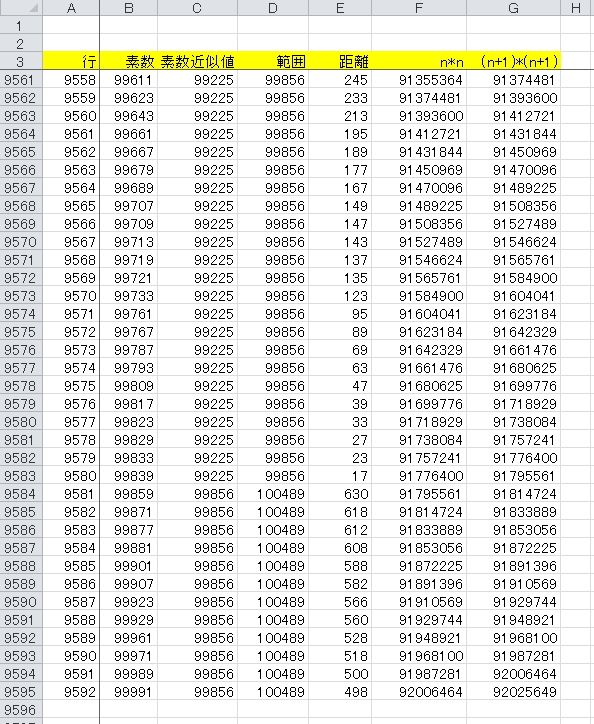
A列）通し番号
B列）素数
C列）素数近似値、素数が n²に近い小さい数値
D列）範囲、n² から (n + 1)²
E列）距離、範囲の²から素数を引いたもの
F列）n²
G列）(n + 1)²

セルC4）=VLOOKUP(B4,F:G,1,1)
セルD4）=VLOOKUP(C4,F:G,2,0)
セルE4）=D4-B4
セルF4）=A4*A4
セルG4）=(A4+1)*(A4+1)

解説 先にF列（n²）とG列（(n + 1)²）を取得するとわかりやすいです

セルC4）=VLOOKUP(B4,F:G,1,1)
VLOOKUP関数を最後の数字を1にすることでVLOOKUP関数は近似値を取得します
例）素数97のとき近似値は81

セルD4）=VLOOKUP(C4,F:G,2,0)
近似値は n²なので範囲の（(n + 1)²を取得します
例）
素数73のとき近似値は64、64がn²のとき81
距離は8の距離とは²のとき81から素数73を引いた値です
この距離が+の場合範囲内で-の場合範囲から出たことになります

つまり
E列が + ならば「 n² とG列 (n + 1)² に素数を含みます」
E列が - ならば「 n² とG列 (n + 1)² にその素数は含まれません」

H列でも作って○×判定させようと思いましたが
確認が面倒なので=SMALL()関数を使って最小値を出してみました



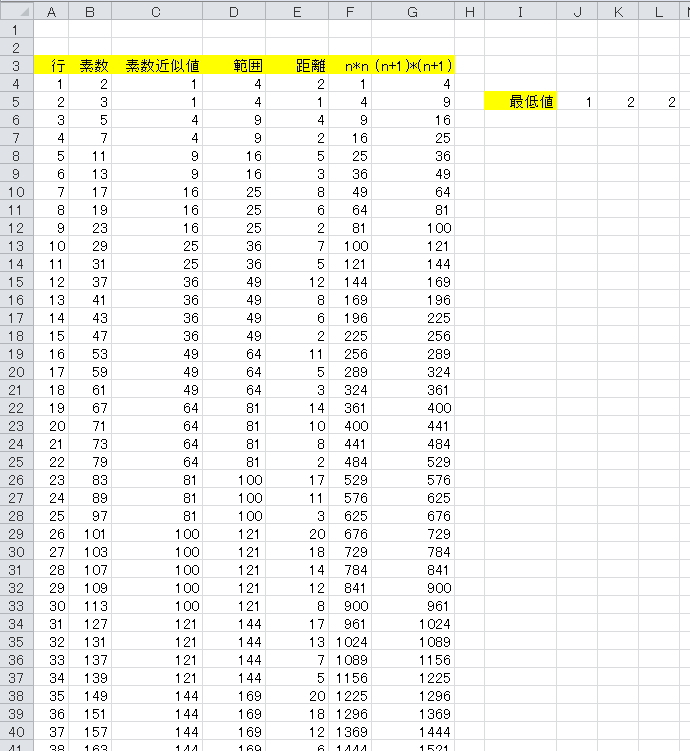
E列にマイナスの数値はありません
今回準備した素数9592個はすべて n²）から（(n + 1)²に含まれます

式をよく考えれば
「素数の近似値」を取得した時点でそれは範囲に含まれています

E列がマイナスになるということは近似値は次の近似値にいってるはずですから
どんな数字でもマイナスになりません

問題は n²がすべて使われているか、ということになります

そんな関数は思いつきません。ですから
1列追加して素数近似値が n²が何回使われているか取得します
この値が 0 なら使われていないことになります



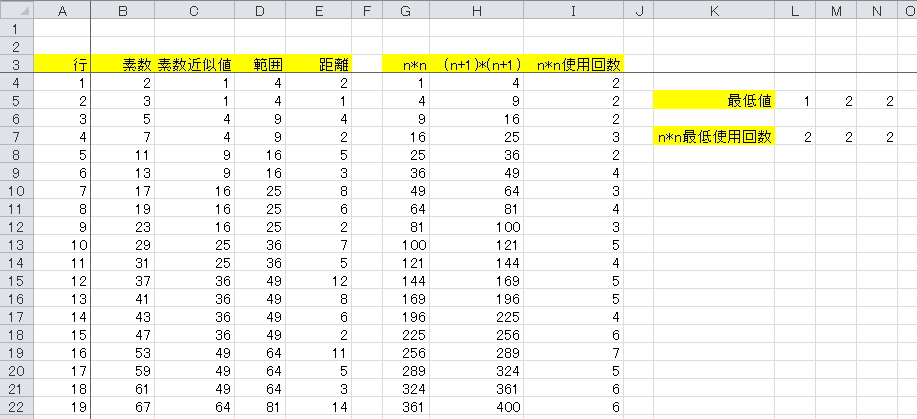
n*n最低使用回数（=SMALL(I:I,1)）の最低値は2で
0ではないのですべて使われています



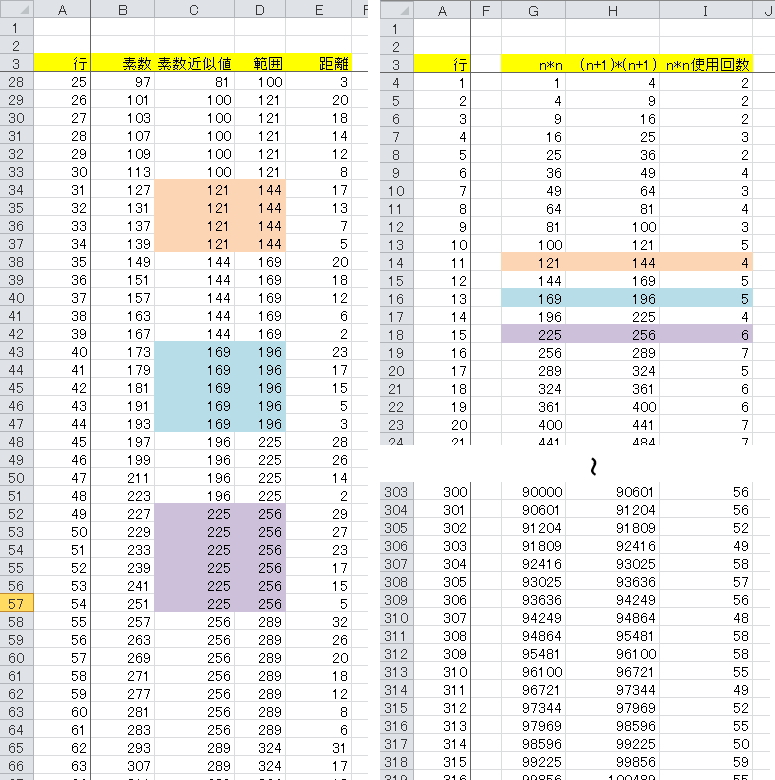
色分けしたのは同じ範囲にある素数の数（n*n使用回数）です

n*n最低使用回数はどんどん増えていきます
このことからn*nの使用回数が0になることはありえないと考えます

表をわかりやすくしてみました


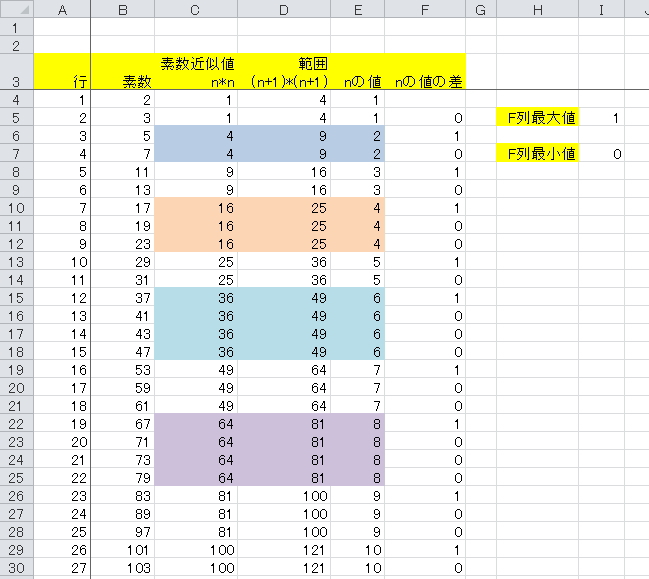
素数の範囲のnの値と1つ前のnの値を引いた値を出しています

これが2以上ならnの値が1つ飛ばしたことになります
数があるので確認のため最大値を出して
念のため戻ることはないか最小値を出してみました

以上のことから分かったことは
素数どころかすべての整数は n²から(n + 1)² に含まれます
そして n²から(n + 1)²の範囲内の素数の数は増え続けるので

任意の自然数 n について、n² と (n + 1)² の間には
必ず素数が存在する。という予想は確実だと思います

---

極端に考えれば
n¹⁰ と (n + 1)¹⁰ の間には必ず素数が存在する

当たり前だと思います
では

n⁹ と (n + 1)⁹ の間には必ず素数が存在する
n⁸ と (n + 1)⁸ の間には必ず素数が存在する
n⁷ と (n + 1)⁷ の間には必ず素数が存在する
n⁶ と (n + 1)⁶ の間には必ず素数が存在する
n⁵ と (n + 1)⁵ の間には必ず素数が存在する
n⁴ と (n + 1)⁴ の間には必ず素数が存在する
n³ と (n + 1)³ の間には必ず素数が存在する

当たり前だと思います
3乗でも範囲が
1～8
8～27
27～64
64～125

n² と (n + 1)² だから微妙なんでしょう

素数から素数の差分より多く増えれば数式はなんでもいいような気がします

素材がもっとあれば、、と思いますが
計算で取得できない素数がベースなのでつまらないです
これ以上頑張る気がしません

以上　ルジャンドル予想でした

---

---

POINT小技
今回のように行が多い場合
1列足したときどうやって10000行コピーするでしょう


普通は図のようにセルの右下の■を下にドラック
数が多ければ？
セルをコピーしてスクロールバーで最下段に行って
Shift押しながら最下段に貼り付けます

ここまでは普通です
実はもっと簡単な方法があります
隣の列がすでに10000行できているのですから
エクセルはそれを自動で判断します

×　図のようにセルの右下の■を下にドラック
〇　右下の■をダブルクリック

これだけでコピーできます
今回のように素数の数が決まっていれば行の長さも決まる
決まってなければあらかじめ通し番号で列を作って置けば
式は全部「右下の■をダブルクリック」でOKです

以上　行数が多いときの小技でした

---

---