なんでも数式で解いてみる「コラッツの問題」 - エクセル関数の使い方

コラッツの問題（コラッツの予想）の規則性を解いてみる

コラッツの問題をご存知でしょうか？

・n が偶数の場合、n を 2 で割る
・n が奇数の場合、n に 3 をかけて 1 を足す

この操作を繰り返すと、どうなるか
「どんな初期値から始めても、有限回の操作のうちに必ず 1 に到達する(そして 1→4→2→1 というループに入る)」という主張が、コラッツの予想である。

グラフにしてみました


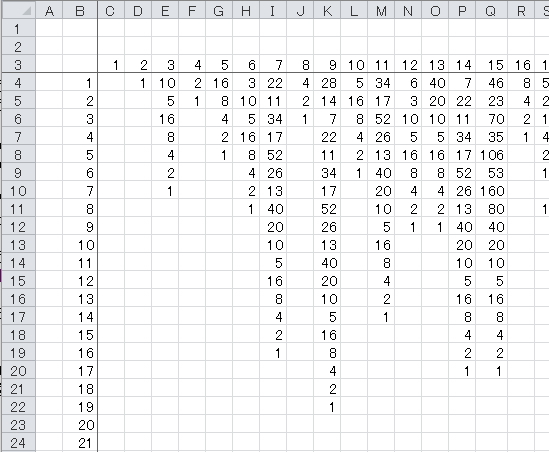
数式は意外と簡単です
セルC4）=IF(OR(C3=1,C3=""),"",IF(ISODD(C3),C3*3*1+1,C3/2))
これを横縦すべてコピーします

ISODD()関数で1つ上のセルを奇数と偶数を判断して
奇数なら3倍して1を足し、偶数なら2で割っています
1を切るとループするので1未満は空白にしています

図は16列ですが1000列200行まで取得してみました
1000までで1番長かったのは「871」で178ステップになります


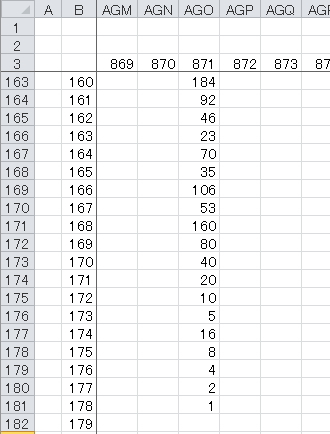
何ステップなのかは規則性はまったく見つかりません

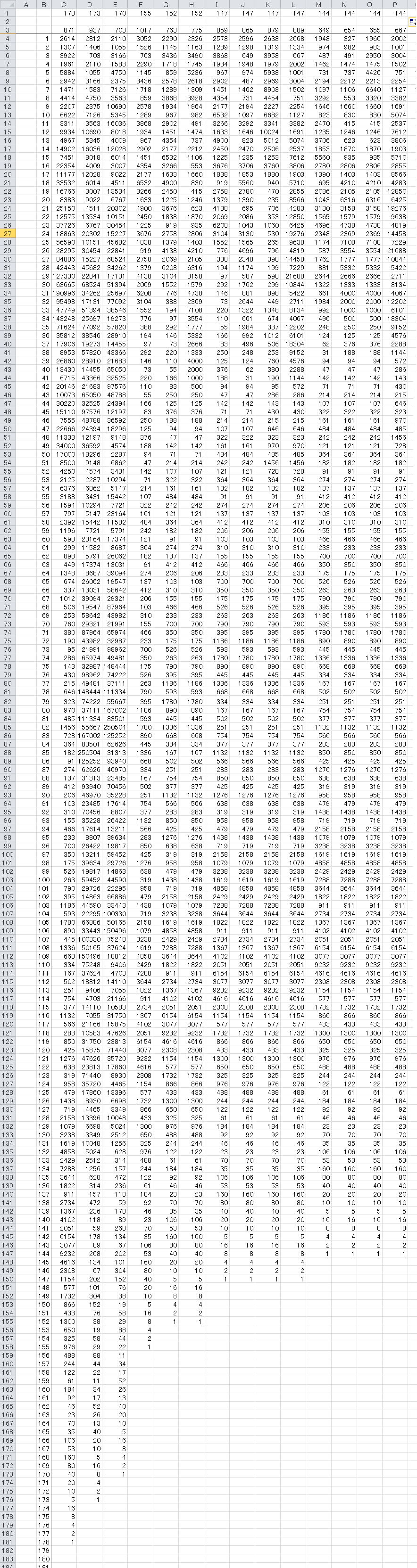
試しに1024列までの長さの1トップ10出してみました
（横の並び替え方法は「縦の並び替えと横の並び替え」を参照してください）

1行目は文字数です
文字数を数えるのはCOUNT()関数です（数値の個数をカウントします）
セルC1）=COUNT(C4:C300)


　数値　文字数　最大値
871178　　190996
937173250504
703170250504
10171559232
7631529232
7751529232
8591479232
8651479232
87914710024
88914721688
6491449232
6541449232
6551449232
66714421688


共通点は・・・・
数値はすべて奇数
最大値はすべて偶数です
数値の偶数は最初から2で割られるので小さくて当たり前と思いますが
小さい数値で割られるのははぶくとするなら

素数最強？

数値に100000までの素数（最大値　99991）を上記の数値に入れてみた



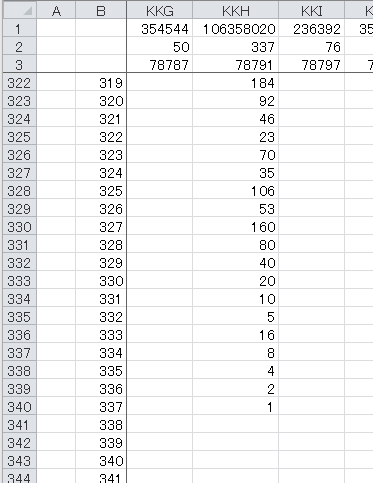
最大ステップ数は
数値：78791
最大値：106358020
ステップ：337

1行目と2行目は探すのが面倒なので
LARGE関数で1番大きい数字を取得
COUNT関数でステップの数を数えています
1行目：D1=LARGE(D4:D1500,1)：D4からD1500で1番大きい数字
2行目：D2=COUNT(D4:D1500)：D4からD1500にある数値の数

行を大きい順に並び変えてみました
（※注意：非力なPCでこの数のセルを並び替えすると固まるかクラッシュします）
（横の並び替え方法は「縦の並び替えと横の並び替え」を参照してください）



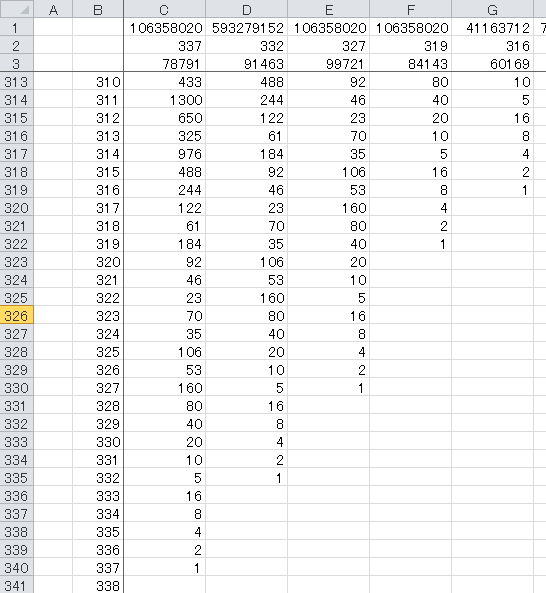
ステップ数トップ5です
　数値　ステップ数　　最大値
78791337　　106358020
91463332593279152
99721327106358020
84143319106358020
6016931641163712


やっぱり
数値は奇数、最大値は偶数です
ここから何か規則性がわかるような気がします
上記は100000までの素数（最大値　99991）素数だけです

何か気づいたら追記します

分かったことは
最短数　2,4,8,16,32,64,128,256・・・
偶数を2で割っているのですから当たり前ですが
最短ステップで終わります



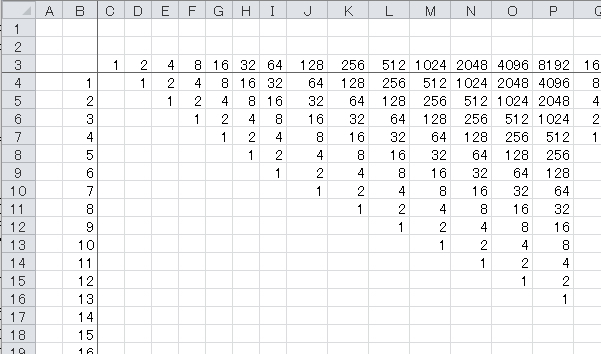
つまりステップ上に1,2,4,8,16,32,64,128,256・・の数字があれば1になるということになります

256で割り切れる数字は必ず1になります
128で割り切れる数字は必ず1になります
64で割り切れる数字は必ず1になります
32で割り切れる数字は必ず1になります
16で割り切れる数字は必ず1になります
8で割り切れる数字は必ず1になります
4で割り切れる数字は必ず1になります
2で割り切れる数字は必ず1になります
1で割り切れる数字は必ず1になります

あれ？「1で割り切れる数字は必ず1になります」
すべての整数は1で割り切れる数字です
ということは
すべての整数は1になります

問題は偶数は2で割るのですから
倍にすれば2の倍数のステップに入るので奇数1も
2の倍数のステップに当てはまります
「2で割り切れる数字は必ず1になります」

2でも1でも割り切れる整数はすべてです

コラッツの予想「必ず 1 に到達する」は正しいようです

私は「必ず 1 に到達する」と思います

追記

コラッツの問題の
「どんな初期値から始めても、有限回の操作のうちに必ず 1 に到達する」
の「有限回」意味ですが、「有限回」を「無限ではない」ととらえるなら

上記の倍にすると1ステップ増えるパターンは
倍倍倍倍倍倍と数億回倍にしてもステップも1桁ずつ増えます
無限に倍倍倍すればステップも無限に増えます
これを「有限回」というか？

倍にした数値から見たら小さい数字ですが
無限の世界ではどうなんでしょう

「有限回」に定数が無く「無限ではない」ととらえるなら
無限数まで到達します

2の倍数ですから必ず1に到達します
でも「有限回の操作のうちに必ず 1 に到達する」
という表現はどうでしょう

倍倍と増えれば確実にステップも増える数字がある以上
有限回というのは当てはまらないと思います

以上を前回と踏まえて
「必ず 1 に到達する」と思いますが
「1 に到達しますが有限回ではない」と思います

以上　コラッツの問題でした
TOP ＞ なんでも数式で解いてみる「フェルマーの最終定理」
(C) 2024 Digital World