なんでも数式で解いてみる「白と黒の比率」
図形の白と黒の比率を求めてみる
今朝テレビを見ていたら下図のような図形が出て
「ABCDの任意に選ばれる黒い部分」と言っていたので
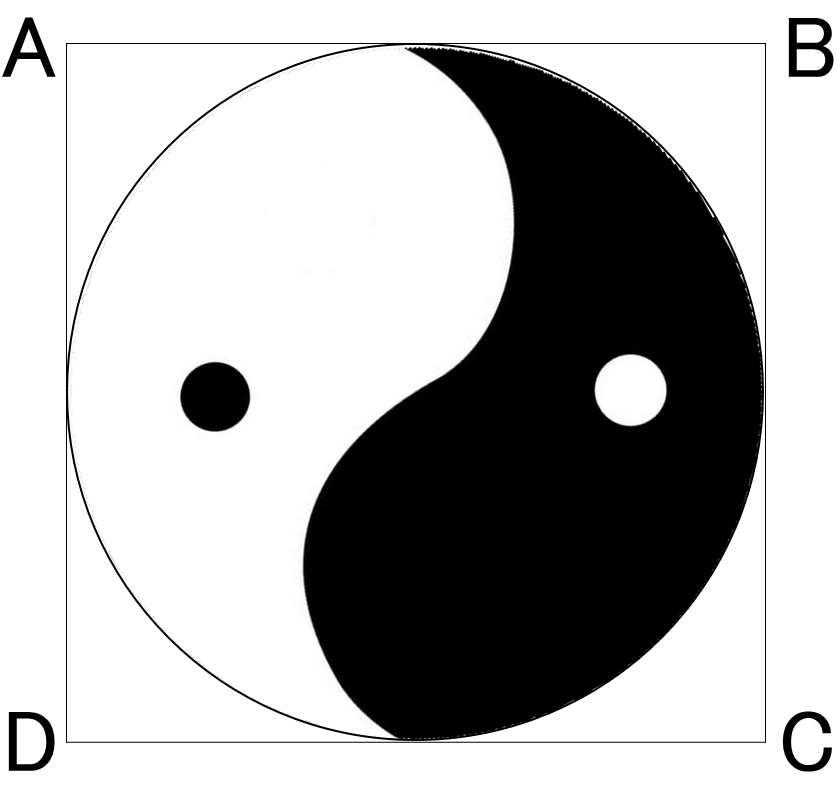
4拓だったので近いのは1/4とわかった
パット見で
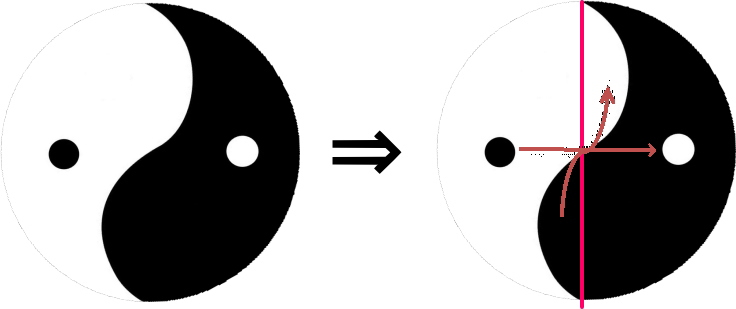
この円を縦に2つにしてはみ出たところを足りないとこに入れれば
きれいに半円です
ここで1/2というのは簡単すぎる
問題は「ABCDの」と言っていました
円の外側があるんです
ここを斜めに切って反転すれば黒がちょっと大きいくらいです
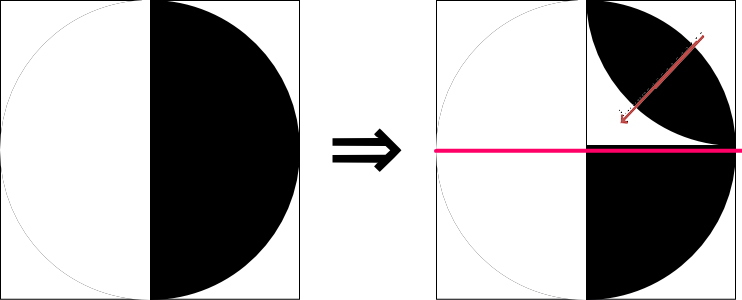
つまり「半分」と「半分の半分」になりますから1/4かなっと
4拓でなければ不正解なのだ実際には
1辺が120mmとして
□の面積 =120*120=14400
●の面積の半分 =(120/2)*(120/2)*3.14/2=5652
つまり黒の比率は
=5652/14400=0.39250
約39.25%になる
これを分数にすると
約4/10
選択肢の1/4は2.5/10
そんなに近くない・・・が
回答は1/8らしい
1/8は1.25/10
さらに遠い
ハッ!そうだ
計算してない部分があります
そう「円の外周の黒い線」です
上記の計算は線が無い場合で
約39.25%になる(正確には 3600π)
もし黒が1/8の場合(12.5%)です
(円の中は小さくても大きくても円の面積の半分です)
円の外周の線は線が1mmの場合
〇の面積の =(120/2)*(120/2)*3.14=11304.00000
1mm引いた場合 =(118/2)*(118/2)*3.14=10930.34
線の面積 =11304.00000-10930.34=373.66
なんと 373.66(3.7366%)です
線だけなら 3.345287159(3.7366%)
1mmベースに考えていこうと思ったのですがまさかの結果が
〇の外周 =(120/2)*(120/2)*3.14=11304.00
〇の内側 =(118/2)*(118/2)*3.14=10930.34
〇の内側の面積の半分 =(118/2)*(118/2)*3.14/2=5465.17000
〇の線の面積 =11304.00000-10930.34=373.66
黒の面積 =5465.17000+5465.170=10930.34000
黒の比率 =5838.83/10930.34=0.53419
線が1mmの場合 53.419 %
増えてるじゃん・・・
そういえば選択肢に1/2ってあったけど
円の中だけなら1/2なのでひっかけ問題かと思ったが
53.419 %なら1/2が1番近いですね
どうしても1/8にしたい場合黒の比率は53.419 %ですから
直径が 42.426407でないと12.5%になりません
実寸で出してみました
1mm=1pxで出しています
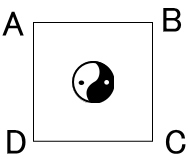
これで
黒の比率1/8です
今朝のと違うなぁ
まっいいか
以上 白と黒の比率でした
表計算や集計で使う関数