なんでも数式で解いてみる「ブロカールの問題」

ブロカールの問題をご存知でしょうか？

n!+1=m²
を満たす自然数 n が存在するか、という数学の問題である。 すでに上式を満たす (n, m) の組はブラウン数と呼ばれ
3つの組み合わせが見つかっています

・(4,5)　4*3*2*1=5*5　=25
・(5,11)　5*4*3*2*1=11*11　=121
・(7,71)　7*6*5*4*3*2*1=71*71　=5041

表にしてみました


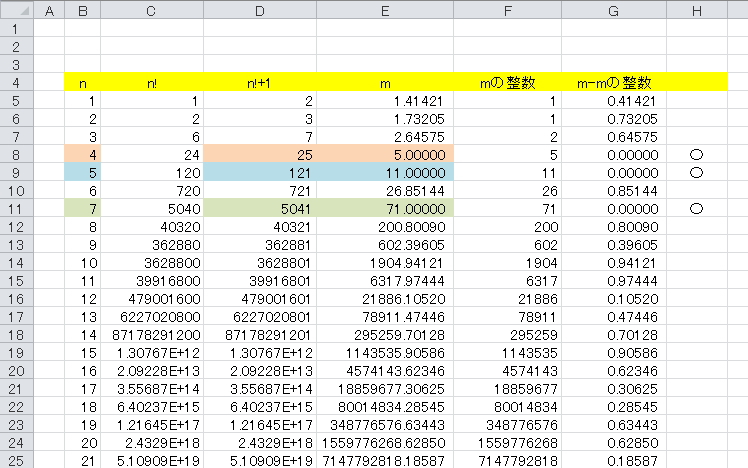
B列）nの数値。1からはじまる整数です
C列）nの階乗。セルC6）=B6*B5
D列）nの階乗+1。セルD5）=C5+1
E列）mの値、（nの階乗+1）の平方根　セルE5）=SQRT(D5)
F列）（nの階乗+1）の平方根の整数部分　セルF5）=INT(E5)
G列）（nの階乗+1）の平方根の小数点以下　セルG5）=E5-F5
H列）小数点以下が0か判定　セルH5）=IF(G5=0,"〇","")

H列に〇がついた行が条件を満たす行になります
色のついたセルはブラウン数の3つの組み合わせです

これをずいっと下にコピーすれば・・・
と思ったのですが
27行ほどでエクセルでは計算できなくなりました


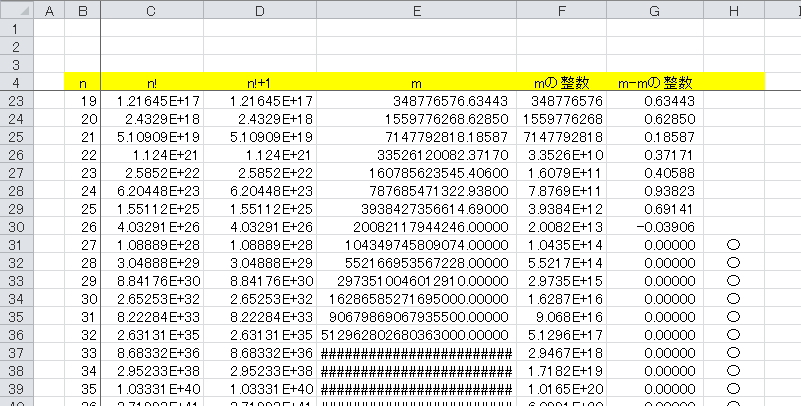
なぜ？
数字を全部表示させてみた


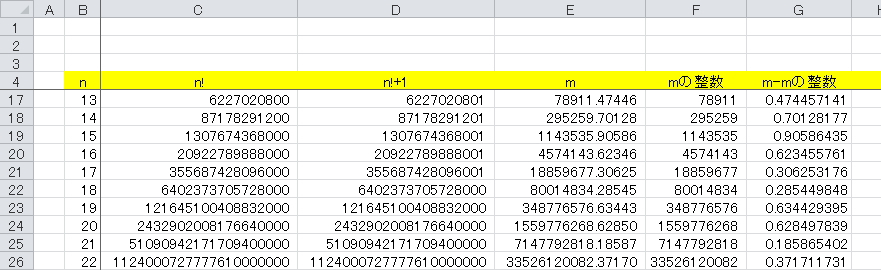
17行目までは
「355687428096000」に1が足されています「355687428096001」
18行目
「6402373705728000」「6402373705728000」足されていません
エクセルでは左から16文字目が五捨六入されます
大きい数字同士の掛け算とかなら構わないのですが
今回のように階乗されて増えていく数字に1を足すのは
エクセルでは17行が限界です

17行で分かったことは
ブラウン数の3つの組み合わせが正しい
ということだけです

以上　ブロカールの問題でした

---

追記

なんだか結論が納得いかなかったので再度考える
が・・
上記のやり方では17行までしか取得できません

まったく違った方向から考えます

階乗の下桁にに注目してみました
表を見た通り10行を超えたとき1桁繰り上がって下2桁は00です
ここからは下2桁は00で行数が増えると0も増えます

「 n!+1 」は1を足しますから下2桁は01です

平方根のルールです
x の下2桁が01の時 x² の下2桁は01になります
x の下3桁が001の時 x² の下3桁は001になります
x の下4桁が0001の時 x² の下4桁は0001になります



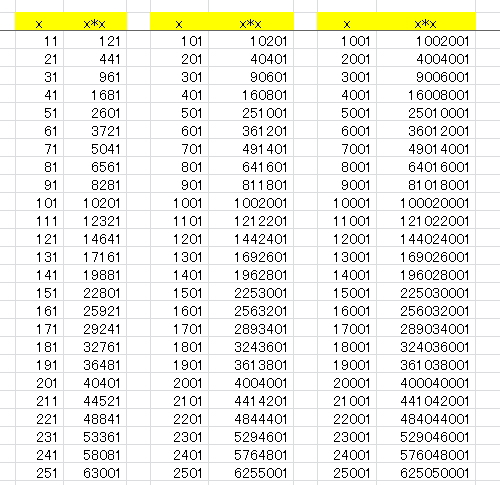
01の時の平方根の最低値は10201です
001の時は1002001
0001の時は100020001
00001の時は10000200001

階乗は下桁が5と0の時0が増えます
5の階乗は120
10の階乗は3628800
15の階乗は1307674368000
20の階乗は2432902008176640000

10の階乗3628800に1を足して3628801
この平方根（下桁01）の最低値は10201

15の階乗1307674368000に1を足して1307674368001
この平方根（下桁001）の最低値は1002001

15の階乗+1の平方根（下桁001）1002001を
10の階乗3628800が上回っています

積である階乗から0が減ることはありえません
15の階乗1307674368000で3つ0があれば
15を超えたら下桁は000（0が3つ）以上でないと成り立ちません

10の階乗のときから桁が上がる15の階乗まで
最低値は10201以上～最高値は1002001未満
この範囲にないと下桁が001と0が増えてしまいます

15の階乗から20の階乗の場合
最低値は1002001以上～最高値は100020001未満
この範囲にないと下桁が0001と0が増えてしまいます

なんかめんどくさい言い方してますが
簡単に言うと

下桁の0の数に注目して
階乗の0の増える数に
平方根の条件が満たさない

ということです。このことから私は

この問題
「n!+1=m² を満たす自然数 n が存在するか」は
下桁に00がつく10行目以降では平方根の条件が満たさないのでありえない

と考えます

※10行目までは表を見た通リ3つの組み合わせが見つかっています

数字が大きすぎてエクセルで検証できませんから
確実とは言えないので、Takao予想ってことにしておきます（ぉぃ

以上　追記ブロカールの問題でした

---

---